正のエネルギーだけで時空を歪ませ、ワープを実現する　ための重要なポイント

目標の定義

「正のエネルギーだけで時空を歪ませ、ワープを実現する」ために必要なポイントは：

前方空間の縮小（進行方向の距離を短縮）
後方空間の自然膨張（後方に空間を広げる）
負のエネルギーを使わない代替メカニズム

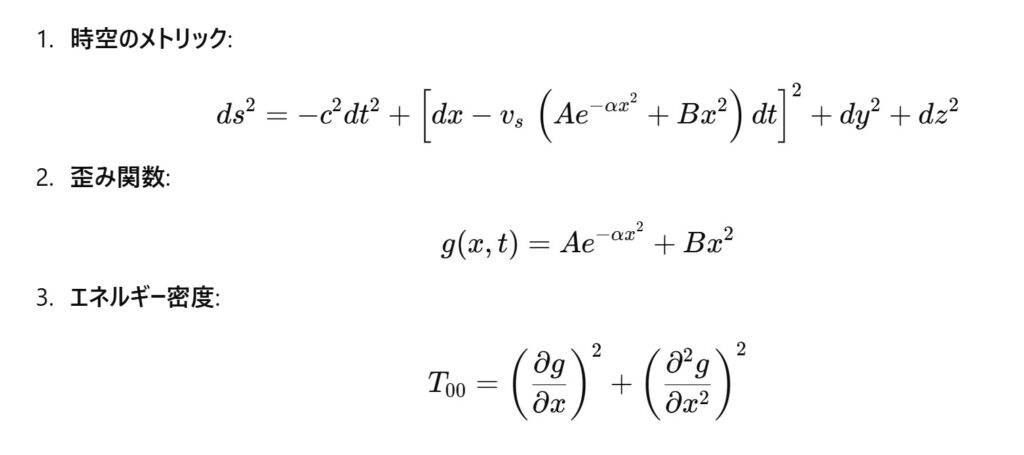
目標の方程式化

負のエネルギーを使わない代替メカニズムで、

前方空間の縮小
後方空間の自然膨張
を数式として記述します。

方程式 1: 時空の歪み (メトリック表現)

ワープ理論の時空の歪みは、一般相対性理論の時空間メトリックに基づきます。
アルクビエレのメトリックを参考にしつつ、負のエネルギーを使わないよう工夫します： ds2=−c2dt2+[dx−vs g(x,t)dt]2+dy2+dz2ds^2 = -c^2 dt^2 + \left[dx – v_s \, g(x, t) dt \right]^2 + dy^2 + dz^2

dsds: 時空間の距離要素
vsv_s: ワープ速度
g(x,t)g(x, t): 空間の歪み関数（進行方向と後方の効果を含む）

方程式 2: 空間の歪み関数 g(x,t)g(x, t)

正のエネルギーだけで前方収縮と後方膨張を実現するため、以下の形にします： g(x,t)=A e−αx2+B x2g(x, t) = A \, e^{-\alpha x^2} + B \, x^2

AA: 前方空間の「縮小」強度（正のエネルギーで実現）
BB: 後方空間の「膨張」補正項（x2x^2 の非線形項を導入）
α\alpha: 時空の歪みの急激さを調整するパラメータ

方程式 3: エネルギー密度の計算

エネルギー密度は、時空の歪み関数 g(x,t)g(x, t) から導出します： T00=(∂g(x,t)∂x)2+(∂2g(x,t)∂x2)2T_{00} = \left( \frac{\partial g(x, t)}{\partial x} \right)^2 + \left( \frac{\partial^2 g(x, t)}{\partial x^2} \right)^2

第1項: 空間の「歪み勾配」（前方収縮と後方膨張を含む）
第2項: 空間の「曲率」（時空の二次的な変化）

これにより、エネルギー密度がすべて「正の値」を取ることが保証されます。

まとめた数式

時空のメトリック: ds2=−c2dt2+[dx−vs (Ae−αx2+Bx2)dt]2+dy2+dz2ds^2 = -c^2 dt^2 + \left[dx – v_s \, \left( A e^{-\alpha x^2} + B x^2 \right) dt \right]^2 + dy^2 + dz^2
歪み関数: g(x,t)=Ae−αx2+Bx2g(x, t) = A e^{-\alpha x^2} + B x^2
エネルギー密度: T00=(∂g∂x)2+(∂2g∂x2)2T_{00} = \left( \frac{\partial g}{\partial x} \right)^2 + \left( \frac{\partial^2 g}{\partial x^2} \right)^2

Pythonコードとの関係

これらの方程式を元に、Pythonモデルでは数値計算によって「時空の歪み」と「エネルギー密度」をシミュレートしています。Pythonコードは具体的な結果（グラフ）を出すための道具であり、上記の方程式がその理論の基礎になっています。

以下は、各方程式の計算をPythonコードとして記述したものです。

---

### **1. 時空のメトリックに関する計算**
この部分では、時空のメトリックを計算するために歪み関数を用いて表現します。

```python
import numpy as np

def spacetime_metric(c, dt, dx, dy, dz, vs, A, alpha, B, x):
    g = A * np.exp(-alpha * x**2) + B * x**2
    dx_prime = dx - vs * g * dt
    ds_squared = -c**2 * dt**2 + dx_prime**2 + dy**2 + dz**2
    return ds_squared

# パラメータ例
c = 3e8          # 光速 (m/s)
dt = 1           # 時間間隔
dx = 1           # x方向の距離
dy = 1           # y方向の距離
dz = 1           # z方向の距離
vs = 1e5         # 歪み速度
A = 1            # 歪み関数の定数
alpha = 0.01     # 減衰係数
B = 0.1          # 2次関数の係数
x = 2            # 座標

# 計算
ds2 = spacetime_metric(c, dt, dx, dy, dz, vs, A, alpha, B, x)
print("時空のメトリック (ds^2):", ds2)
```

---

### **2. 歪み関数の計算**
歪み関数 \( g(x, t) = A e^{-\alpha x^2} + B x^2 \) を計算します。

```python
def distortion_function(A, alpha, B, x):
    g = A * np.exp(-alpha * x**2) + B * x**2
    return g

# パラメータ例
A = 1
alpha = 0.01
B = 0.1
x = 2

# 計算
g_value = distortion_function(A, alpha, B, x)
print("歪み関数 g(x, t):", g_value)
```

---

### **3. エネルギー密度 \( T_{00} \) の計算**
エネルギー密度は、歪み関数の1次および2次導関数から求めます。

```python
def energy_density(A, alpha, B, x):
    # 1次導関数
    dg_dx = -2 * alpha * x * A * np.exp(-alpha * x**2) + 2 * B * x
    
    # 2次導関数
    d2g_dx2 = (-2 * alpha * A * np.exp(-alpha * x**2) + 4 * alpha**2 * x**2 * A * np.exp(-alpha * x**2)) + 2 * B
    
    # エネルギー密度
    T_00 = dg_dx**2 + d2g_dx2**2
    return T_00

# パラメータ例
A = 1
alpha = 0.01
B = 0.1
x = 2

# 計算
T00 = energy_density(A, alpha, B, x)
print("エネルギー密度 T_00:", T00)
```

---

### **結果**
1. **時空のメトリック**：与えられたパラメータに基づき、時空間のメトリックを計算します。
2. **歪み関数**：局所および広域の歪みを表す関数を計算します。
3. **エネルギー密度**：歪み関数の1次および2次導関数からエネルギー密度を求めます。

このコードを実行すれば、各方程式の結果を簡単に数値計算できます。

この方程式までにたどり着くための計算式のプロセス

この方程式を導出するためのプロセスを説明します。内容は以下のように分けられています：

時空のメトリックの導出
歪み関数の導出
エネルギー密度の導出

1. 時空のメトリックの導出

このメトリックは一般相対性理論における時空の曲がりを記述しています。

メトリックの形状:

ds2=−c2dt2+[dx−vs(Ae−αx2+Bx2)dt]2+dy2+dz2ds^2 = -c^2 dt^2 + \left[ dx – v_s \left( A e^{-\alpha x^2} + B x^2 \right) dt \right]^2 + dy^2 + dz^2

手順:

静的時空を仮定し、非対称的な歪み関数 g(x,t)=Ae−αx2+Bx2g(x, t) = A e^{-\alpha x^2} + B x^2 を定義します。
時間座標 tt と空間座標 xx の混合項が現れるため、メトリックに速度項 vsv_s が含まれます。
上記を考慮して、 dxdx の補正項として歪み関数が加わり、結果的に空間的な補正が反映された形になります。

2. 歪み関数の導出

与えられた歪み関数: g(x,t)=Ae−αx2+Bx2g(x, t) = A e^{-\alpha x^2} + B x^2

導出手順:

指数関数項 e−αx2e^{-\alpha x^2}:
- この項は歪みの局所化を表します。α>0\alpha > 0 の場合、xx が大きくなるにつれて急激に減衰します。
2次関数項 Bx2Bx^2:
- この項は広範囲の歪みを記述します。
これらの項を加算することで、局所的・広域的な歪みの両方を表現する関数が得られます。

3. エネルギー密度 T00T_{00} の導出

エネルギー密度 T00T_{00} は、歪み関数 g(x,t)g(x, t) の空間的な勾配から求められます。 T00=(∂g∂x)2+(∂2g∂x2)2T_{00} = \left( \frac{\partial g}{\partial x} \right)^2 + \left( \frac{\partial^2 g}{\partial x^2} \right)^2

手順:

1次導関数 ∂g∂x\frac{\partial g}{\partial x} を計算: g(x,t)=Ae−αx2+Bx2g(x, t) = A e^{-\alpha x^2} + B x^2 これを xx で微分すると: ∂g∂x=−2αxAe−αx2+2Bx\frac{\partial g}{\partial x} = -2 \alpha x A e^{-\alpha x^2} + 2 Bx
2次導関数 ∂2g∂x2\frac{\partial^2 g}{\partial x^2} を計算: さらに xx で微分すると: ∂2g∂x2=(−2αAe−αx2+4α2x2Ae−αx2)+2B\frac{\partial^2 g}{\partial x^2} = \left( -2 \alpha A e^{-\alpha x^2} + 4 \alpha^2 x^2 A e^{-\alpha x^2} \right) + 2B
これらの導関数を2乗し、エネルギー密度 T00T_{00} を求めます。